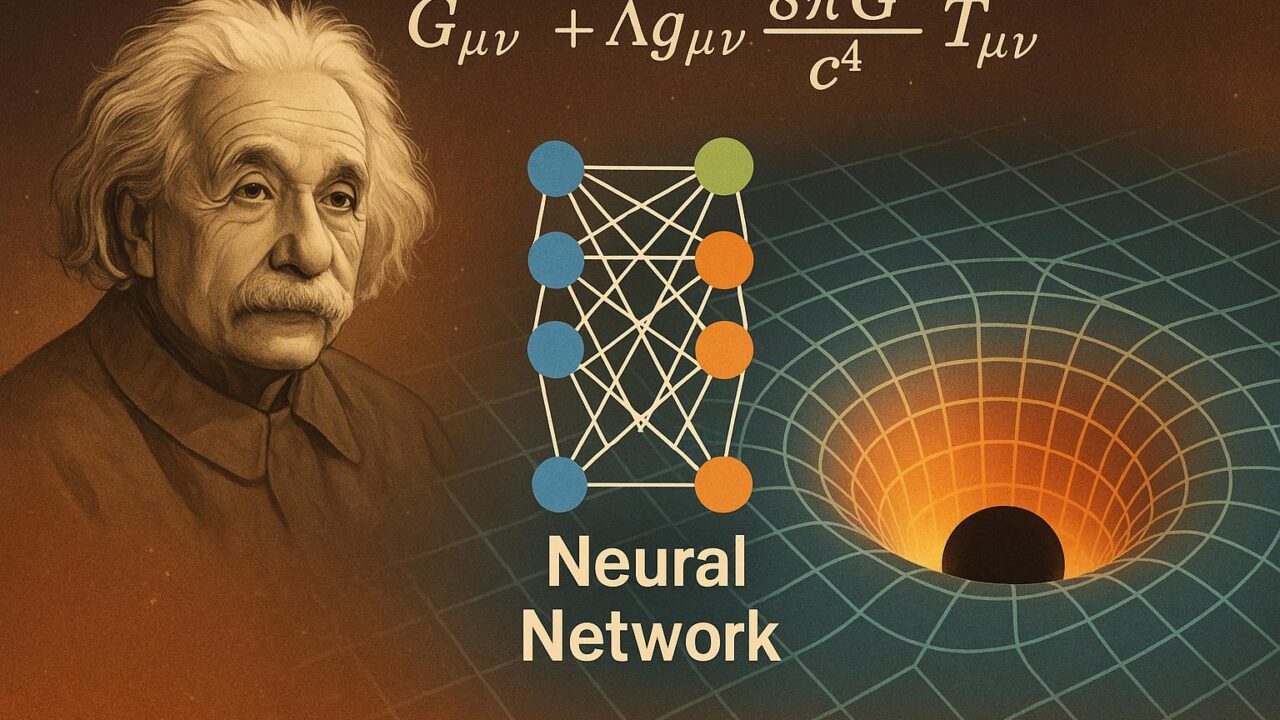
現代物理学において、アインシュタインの一般相対性理論は、宇宙の大規模構造や重力波の理解、ブラックホールの性質解明など、多くの最先端研究の基礎を為す理論です。しかし、この一般相対性理論の核心にあるアインシュタイン方程式を数値的に解くことは極めて難解で、長らく数値相対論と呼ばれる専門分野の専門家の手に委ねられてきました。複雑な幾何学構造、大量の計算量、高い数学的理解が求められるため、多くの応用に取り組む際の障壁ともなっていました。
こうした中、近年のディープラーニング技術の発展によって数値計算の在り方そのものが大きく変わりつつあります。ニューラルネットワークが偏微分方程式を解く新しい道具として注目されるようになる中、「Einstein Fields: A Neural Perspective To Computational General Relativity」と題された研究が登場しました。この研究は、一般相対論の数値計算における大きなパラダイムシフトを提案するものであり、物理学と機械学習の融合が新たな可能性を開こうとしていることを端的に示しています。
本記事では、この研究の概要と意義、技術的なアプローチ、そして今後の展望について詳しく解説していきます。
ニューラルネットワークと偏微分方程式
まず、本研究の背景となる技術の理解を深めるために、ニューラルネットワークがどのように偏微分方程式の解法に応用されているかを簡単に見ておきましょう。
従来の数値計算法では、時間や空間を離散化し、数値的な差分をとって解をコツコツと求めていく必要がありました。しかし、ニューラルネットワーク、特に物理情報を組み込んだニューラルネットワーク(PINNs: Physics-Informed Neural Networks)では、方程式の解となる関数そのものをネットワークが学習によって近似し、それを訓練することで偏微分方程式の近似解を得ることが可能になります。
このアプローチの利点は、格子点による離散化が不要で、連続的な空間領域全体にわたる滑らかな解を捕える柔軟性、そして不均質や非線形な問題にも比較的容易に対応できる高い表現力にあります。
「Einstein Fields」の革新性
「Einstein Fields」というこの研究は、一般相対性理論におけるコア方程式、すなわちアインシュタイン場の方程式をニューラルネットワークベースで直接解くことを目的としています。
一般相対論において、時空の構造はエネルギーと運動量の分布に応じて湾曲するとされ、その関係がアインシュタイン方程式で記述されます。方程式自体は非線形かつ高次の偏微分方程式であり、計算資源と精度の両面で重い負担を強いられます。特にブラックホール同士の衝突や、重力波の放出を取り扱うようなケースでは、その難易度が一気に跳ね上がります。
本研究では、ディープラーニングによってこの問題に新たな角度から挑戦しています。アプローチのポイントは以下の通りです。
1. 自然な幾何構造を尊重したネットワーク設計:
研究では、時空の幾何構造におけるテンソル場(メトリクステンソルなど)を直接学習の対象とするために、固有の幾何的構造を持つニューラルネットワークアーキテクチャを設計しています。これにより、物理的整合性を損なうことなく、方程式の近似解を学習過程に組み込むことができます。
2. 方程式の制約を損失関数として組み込む:
アインシュタイン方程式の構造はネットワークの出力そのものに直接的な制約を課します。つまり、モデルはただの数値予測ではなく、「物理法則を満たすように」出力することを求められます。損失関数の中に方程式の残差を含めることで、この物理的制約を自己教師信号として強制しているのです。
3. 初期条件や境界条件の統合:
一般相対性理論の問題設定では、時間発展の前提として与えられる初期条件、また空間領域における境界条件が重要な役割を果たします。本手法では、こうした条件もニューラルネットワーク学習の訓練信号として組み込み、解が物理的妥当性を保つよう調整されます。
実際の応用:シュヴァルツシルト解の復元
本研究の妥当性を示すテストケースとして、最も基本的かつ重要な時空解の一つである「シュヴァルツシルト解」が用いられています。これは静的で球対称な真空解であり、ブラックホールの外側領域に対応します。
研究者らは、この解をニューラルネットワークで再現可能であることを実証しました。ネットワークは初期状態から学習を開始し、徐々にシュヴァルツシルト解に収束していく様子が観測され、また計算誤差も従来の数値解法と比較しても精度の高いものとなっています。
この成果は、従来の差分法や有限要素法が用いていた手法とは一線を画し、連続的な関数空間上で解を近似する新しい時空解法の道を切り開くものです。
計算効率と将来の展望
ニューラルネットワークによる方程式解法は、初期のトレーニングにかかる計算コストこそ必要ですが、一旦学習されたモデルは非常に高速に新たな入力に対して応答を返すことができるという利点があります。この特性は、例えば多くのパラメータ空間を探索する必要がある理論宇宙論の研究や、即時応答が求められる天体観測データの処理などにおいて非常に有力な手段となる可能性があります。
さらに、マルチスケール現象やカオス的な時間発展を巻き込む問題、あるいは次元数がさらに高い理論モデルへの応用も視野に入る中、今回のアインシュタイン方程式への応用は、その第一歩に過ぎないとも言えるでしょう。
また、研究に用いられているネットワーク構造やトレーニング手法は、他の場面でも流用可能であり、広く物理学における計算方法論の基礎を塗り替える可能性を持っています。
今後の課題
もちろん、現段階では万能な手法とは言えません。特に、時空の特異点や非常に急峻な勾配を伴うようなスパイク構造のある解に対しては、ニューラルネットワークの学習が安定しない可能性も指摘されています。また、トレーニングデータの選び方、学習率の調整、モデル容量の制限など、機械学習に固有の問題も数値相対論に組み込まれる形になるため、新たなベストプラクティスの確立が求められます。
物理的観点からも、学習済みモデルが本当に因果律やエネルギー保存則といった根本原理を自動で守るのか、あるいは目に見えないところでズレが生じていないかという懸念もあり、理論と実装の間のギャップをいかに取り除くかが重要な研究課題となるでしょう。
結びに
「Einstein Fields: A Neural Perspective To Computational General Relativity」は、一般相対性理論という難解な理論を、最先端の機械学習技術の助けを借りてより身近なものにし、宇宙の深奥に迫る新たな手段を提示しています。それは単なる技術的改良を超え、物理法則の理解と計算科学の融合という新しい時代の幕開けを象徴しています。
このアプローチはまだ発展途上ですが、今後の継続的な研究により、多くの未知の現象が新しい視点から明らかになっていくことでしょう。物理とAIの融合、そしてそれによって可能になる科学の未来に、我々はますます大きな期待を寄せることができます。